Hãy tưởng tượng bạn đang ngồi trên một chiếc xe và người lái đột ngột nhấn ga, bạn cảm thấy mình bị đẩy mạnh về phía sau. Hoặc khi bạn thả một vật gì đó, nó không chỉ rơi mà còn rơi nhanh dần. Điều gì đứng sau những thay đổi đầy kịch tính về vận tốc ấy? Đó chính là gia tốc – một khái niệm trung tâm trong vật lý, là đại lượng mô tả mức độ "tăng tốc" hay "giảm tốc", thậm chí là sự thay đổi hướng chuyển động. Từ những chuyển động đơn giản nhất quanh ta đến những hiện tượng phức tạp trong vũ trụ, gia tốc đóng vai trò then chốt. Nhưng làm thế nào để nắm bắt trọn vẹn bản chất của nó, phân biệt các loại gia tốc khác nhau, và áp dụng chúng vào việc giải thích thế giới vật lý?
Gia tốc không chỉ là tăng tốc
Tưởng tượng bạn đang ngồi trên một chiếc xe hơi. Khi bác tài nhấn ga, bạn cảm thấy mình bị đẩy về phía sau, xe chạy nhanh dần lên. Lúc bác tài phanh gấp, bạn lại bị chồm người về phía trước, xe chạy chậm dần. Hoặc khi xe vào cua, dù tốc độ có thể không đổi, bạn vẫn cảm thấy một lực đẩy mình sang bên. Tất cả những cảm giác đó đều liên quan đến một đại lượng vật lý cực kỳ quan trọng: gia tốc.
Vậy gia tốc là gì? Đơn giản nhất, gia tốc là thước đo cho biết vận tốc của một vật thay đổi nhanh hay chậm theo thời gian. Nó không chỉ nói về việc vật đó có đang chạy nhanh lên hay không, mà còn bao gồm cả việc nó đang chạy chậm lại hay thậm chí là thay đổi hướng chuyển động. Nếu vận tốc không thay đổi gì cả (cả về độ lớn lẫn hướng), thì gia tốc bằng không.
Đơn vị đo của gia tốc trong hệ đo lường quốc tế (SI) là mét trên giây bình phương (m/s²). Nghĩa là, vận tốc của vật thay đổi bao nhiêu mét trên giây, trong mỗi giây. Ví dụ, gia tốc 2 m/s² có nghĩa là cứ sau mỗi giây, vận tốc của vật tăng thêm 2 m/s.
Một điểm cực kỳ quan trọng cần nhớ là gia tốc là một đại lượng vector. Điều này có nghĩa là nó không chỉ có độ lớn (nhanh hay chậm) mà còn có cả phương và chiều. Chiều của vector gia tốc cho ta biết vận tốc đang thay đổi theo hướng nào.
Đây là lúc sự khác biệt giữa gia tốc và vận tốc trở nên rõ ràng nhất. Vận tốc cho bạn biết vật đang đi nhanh cỡ nào và đi về hướng nào tại một khoảnh khắc nhất định. Nó là trạng thái chuyển động hiện tại. Còn gia tốc lại nói về sự thay đổi của vận tốc đó.
Hãy hình dung thế này:
- Bạn đang đi bộ với vận tốc 5 km/h về phía trước. Vận tốc của bạn là một vector có độ lớn 5 km/h và hướng về phía trước.
- Bây giờ bạn bắt đầu chạy nhanh hơn. Vận tốc của bạn tăng lên 6, 7, 8 km/h… Sự tăng lên này chính là do bạn có gia tốc cùng chiều với vận tốc.
- Nếu bạn dừng lại đột ngột, vận tốc giảm từ 8 xuống 0 km/h. Lúc này bạn cũng có gia tốc, nhưng nó lại ngược chiều với vận tốc ban đầu, khiến bạn chậm lại.
- Còn nếu bạn đang chạy đều 10 km/h nhưng bỗng nhiên rẽ sang trái, vận tốc của bạn vẫn có độ lớn 10 km/h nhưng hướng đã thay đổi. Sự thay đổi hướng này cũng cần có gia tốc, dù độ lớn tốc độ có thể không đổi.
Nói tóm lại, vận tốc là "bạn đang đi đâu và nhanh thế nào ngay bây giờ", còn gia tốc là "bạn đang thay đổi cái ‘đi đâu và nhanh thế nào’ đó ra sao". Một vật có thể có vận tốc rất lớn nhưng gia tốc bằng không (chuyển động thẳng đều), hoặc vận tốc bằng không nhưng vẫn có gia tốc (ví dụ: một quả bóng được ném lên đến điểm cao nhất, vận tốc tức thời bằng 0 nhưng gia tốc trọng trường vẫn đang kéo nó xuống). Hiểu được sự khác biệt này là chìa khóa để làm chủ các bài toán về chuyển động trong vật lý.
Gia tốc: Nhiều hơn bạn nghĩ
Sau khi đã nắm được khái niệm cơ bản về gia tốc – thước đo sự thay đổi vận tốc, bạn có biết rằng "gia tốc" không chỉ có một kiểu duy nhất? Tùy thuộc vào cách vật thể di chuyển và yếu tố nào đang tác động, chúng ta sẽ gặp những "gương mặt" khác nhau của gia tốc. Bạn có bao giờ thắc mắc tại sao cảm giác khi xe tăng tốc trên đường thẳng lại khác với cảm giác bị "đẩy" mạnh vào ghế khi xe cua gấp không? Hay tại sao một quả táo và một viên đá lại rơi xuống đất với cùng một "sự thúc đẩy"? Đó là bởi vì gia tốc biểu hiện dưới nhiều hình thức khác nhau. Cùng khám phá những loại gia tốc phổ biến nhất để hiểu rõ hơn về thế giới chuyển động đầy biến hóa này nhé.
Đo lường sự thay đổi vận tốc Khoảnh khắc hay Khoảng thời gian
Khi nói về gia tốc, chúng ta thường nghĩ ngay đến việc vận tốc đang thay đổi nhanh hay chậm. Nhưng sự thay đổi này có thể được nhìn nhận theo hai cách khác nhau, dẫn đến hai khái niệm quan trọng: gia tốc trung bình và gia tốc tức thời.
Hãy tưởng tượng bạn đang lái xe trên đường. Đôi khi bạn tăng tốc đều đều, nhưng có lúc bạn đạp ga mạnh hơn, rồi lại nhả ra một chút. Vận tốc của xe thay đổi liên tục, không phải lúc nào cũng theo một quy luật nhất định.
Gia tốc trung bình: Cái nhìn tổng quát
Gia tốc trung bình cho chúng ta biết sự thay đổi vận tốc tổng thể trong một khoảng thời gian nhất định. Nó giống như bạn xem bản báo cáo tổng kết hiệu suất của chiếc xe sau một chuyến đi vậy đó.
Công thức tính gia tốc trung bình khá đơn giản:
a_tb = (v_cuối - v_đầu) / (t_cuối - t_đầu)
Hoặc viết gọn hơn là:
a_tb = Δv / Δt
Trong đó:
Δvlà độ biến thiên vận tốc (vận tốc lúc cuối trừ vận tốc lúc đầu).Δtlà khoảng thời gian xảy ra sự biến thiên đó.
Ví dụ, nếu xe của bạn tăng tốc từ 10 m/s lên 20 m/s trong vòng 5 giây, thì gia tốc trung bình trong 5 giây đó là (20 - 10) / 5 = 10 / 5 = 2 m/s². Điều này có nghĩa là, trung bình mỗi giây vận tốc của xe tăng thêm 2 m/s.
Tuy nhiên, gia tốc trung bình không cho bạn biết chuyện gì đang xảy ra tại bất kỳ khoảnh khắc cụ thể nào trong 5 giây đó. Có thể lúc đầu bạn tăng tốc rất nhanh, sau đó lại chậm lại một chút.
Gia tốc tức thời: Bức ảnh chụp nhanh
Để biết chính xác vận tốc đang thay đổi nhanh hay chậm ngay tại một điểm, một khoảnh khắc cụ thể, chúng ta cần đến gia tốc tức thời. Nó giống như bạn chụp một bức ảnh "snapshot" về sự thay đổi vận tốc ngay lúc đó vậy.
Để hình dung gia tốc tức thời, hãy quay lại công thức gia tốc trung bình Δv / Δt. Thay vì xét một khoảng thời gian Δt dài, chúng ta thu nhỏ khoảng thời gian này lại, nhỏ đến mức nó tiến gần về 0. Khi Δt cực kỳ nhỏ, cái tỉ số Δv / Δt này sẽ cho chúng ta biết tốc độ thay đổi của vận tốc ngay tại khoảnh khắc bắt đầu của khoảng thời gian cực nhỏ đó.
Trong toán học, quá trình thu nhỏ Δt về 0 này chính là khái niệm đạo hàm. Vì vậy, gia tốc tức thời được định nghĩa là đạo hàm của vận tốc theo thời gian:
a = dv/dt
Ở đây, dv/dt biểu thị tốc độ thay đổi của vận tốc v ngay tại thời điểm t.
Sự khác biệt cốt lõi
Điểm khác nhau mấu chốt là:
- Gia tốc trung bình: Đo lường sự thay đổi vận tốc trong một khoảng thời gian. Nó là giá trị trung bình, không phản ánh chi tiết từng biến động nhỏ.
- Gia tốc tức thời: Đo lường sự thay đổi vận tốc tại một khoảnh khắc cụ thể. Nó cho biết tốc độ "tăng tốc" hoặc "giảm tốc" chính xác ngay tại thời điểm đó.
Trong thực tế, kim đồng hồ tốc độ (speedometer) trên xe của bạn cho biết vận tốc tức thời. Và nếu có một thiết bị đo gia tốc, nó sẽ cho bạn biết gia tốc tức thời của xe tại mỗi khoảnh khắc.
Hiểu rõ sự khác biệt giữa gia tốc trung bình và tức thời giúp chúng ta phân tích chuyển động một cách chính xác hơn, đặc biệt là trong những trường hợp vận tốc thay đổi không đều.
Gia Tốc Trên Đường Cong Và Vòng Xoay
Khi vật thể không chỉ di chuyển thẳng mà còn "uốn lượn" hay "xoay vòng", câu chuyện về gia tốc trở nên thú vị hơn nhiều. Lúc này, gia tốc không chỉ đơn thuần là làm vật nhanh lên hay chậm đi theo một đường thẳng tắp nữa. Nó còn "ép" vật thay đổi hướng đi, tạo nên những đường cong mềm mại hay những vòng quay chóng mặt.
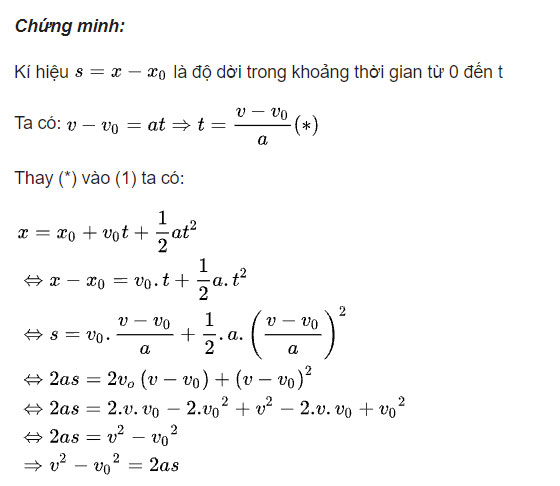
Hãy tưởng tượng bạn đang ngồi trên một chiếc xe đua lao vào khúc cua. Tốc độ của xe có thể thay đổi (nhanh lên hoặc chậm đi), và chắc chắn hướng chuyển động của xe cũng thay đổi liên tục. Gia tốc trong trường hợp này không còn chỉ nằm trên một đường thẳng nữa mà có thể được phân tích thành hai "thành phần" chính, mỗi thành phần đóng một vai trò riêng biệt.
Thành phần đầu tiên là gia tốc tiếp tuyến. Cái tên nói lên tất cả: nó song song (hoặc ngược chiều) với phương chuyển động tức thời của vật, tức là "tiếp tuyến" với quỹ đạo cong tại điểm đó. Vai trò của gia tốc tiếp tuyến cực kỳ rõ ràng: nó làm thay đổi độ lớn của vận tốc. Nếu gia tốc tiếp tuyến cùng chiều với vận tốc, vật sẽ chạy nhanh hơn (tăng tốc). Nếu ngược chiều, vật sẽ chạy chậm lại (giảm tốc). Cứ như bạn đạp ga hay phanh vậy đó!
Nhưng chỉ có gia tốc tiếp tuyến thì vật vẫn cứ đi thẳng hoặc nhanh chậm trên đường thẳng. Để vật "bẻ lái" và đi theo đường cong, cần có một thành phần gia tốc khác. Đó chính là gia tốc pháp tuyến, hay còn gọi là gia tốc hướng tâm. Thành phần này luôn vuông góc với vận tốc và luôn hướng về phía "lõm" của quỹ đạo cong (tức là hướng vào tâm của đường cong đó). Gia tốc pháp tuyến không hề làm thay đổi độ lớn của vận tốc, nó chỉ có một nhiệm vụ duy nhất: làm thay đổi hướng của vận tốc, giữ cho vật bám theo đường cong. Bạn cảm thấy mình bị "ép" vào ghế khi xe vào cua chính là do gia tốc hướng tâm này gây ra.
Tổng hợp lại, gia tốc "thật sự" của vật khi đi trên đường cong chính là tổng vector của gia tốc tiếp tuyến và gia tốc pháp tuyến. Người ta gọi đây là gia tốc toàn phần. Độ lớn và hướng của gia tốc toàn phần sẽ thay đổi tùy thuộc vào việc vật đang nhanh lên hay chậm đi, và độ cong của quỹ đạo.
Còn khi nói về chuyển động quay quanh một trục cố định thì sao? Lúc này, chúng ta quan tâm đến sự thay đổi của tốc độ quay. Đại lượng mô tả sự thay đổi này chính là gia tốc góc. Gia tốc góc cho biết tốc độ quay (vận tốc góc) đang tăng hay giảm nhanh đến mức nào. Nếu gia tốc góc lớn, vật sẽ quay nhanh dần lên rất nhanh. Nếu gia tốc góc nhỏ hoặc bằng không, tốc độ quay sẽ thay đổi chậm hoặc giữ nguyên. Đối với một điểm bất kỳ trên vật đang quay, gia tốc góc có liên hệ trực tiếp với gia tốc tiếp tuyến của điểm đó: điểm nào càng xa tâm quay thì gia tốc tiếp tuyến của nó càng lớn nếu tốc độ quay thay đổi nhanh.
Tóm lại, dù là đi trên đường cong hay quay vòng, gia tốc luôn là "người kể chuyện" về sự thay đổi của vận tốc. Gia tốc tiếp tuyến lo việc nhanh chậm, gia tốc pháp tuyến lo việc bẻ lái, còn gia tốc góc thì điều chỉnh nhịp điệu của cả vòng quay.
Sức hút Trái Đất và gia tốc rơi tự do
Bạn đã bao giờ thả một vật gì đó từ trên cao xuống chưa? Chắc chắn rồi! Và bạn để ý thấy nó không chỉ rơi xuống mà còn rơi ngày càng nhanh hơn, đúng không? Cái "nhanh hơn" đó chính là biểu hiện rõ nhất của một loại gia tốc rất đặc biệt: gia tốc trọng trường, thường ký hiệu là g.

Vậy cái gì khiến mọi thứ rơi nhanh dần về phía Trái Đất? Chính là lực hấp dẫn khổng lồ của hành tinh chúng ta. Trái Đất như một nam châm siêu bự, hút mọi vật thể có khối lượng về phía tâm của nó. Gia tốc trọng trường chính là thước đo cho thấy lực hút này mạnh đến mức nào trong việc làm thay đổi vận tốc của vật khi nó rơi. Hướng của gia tốc trọng trường luôn thẳng đứng, chĩa xuống dưới, hướng về tâm Trái Đất.
Điều thú vị là giá trị của gia tốc trọng trường không phải là một con số tuyệt đối không đổi trên khắp mọi nơi. Nó có thể thay đổi một chút tùy thuộc vào địa điểm bạn đang đứng. Ví dụ, ở gần xích đạo, giá trị của g sẽ nhỏ hơn một chút so với ở hai cực. Leo lên đỉnh núi cao chót vót, g cũng sẽ hơi khác so với khi bạn ở mặt nước biển. Lý do là Trái Đất không phải là một quả cầu hoàn hảo, nó hơi phình ra ở xích đạo, và độ cao so với tâm Trái Đất cũng khác nhau. Tuy nhiên, để tiện tính toán trong hầu hết các bài toán phổ thông, chúng ta thường lấy một giá trị xấp xỉ chuẩn là 9,8 m/s². Con số này nói lên rằng, mỗi giây trôi qua khi vật rơi, vận tốc của nó tăng thêm khoảng 9,8 mét trên giây (nếu bỏ qua sức cản của không khí).
Chính gia tốc trọng trường này là nhân vật chính trong các bài toán vật lý liên quan đến vật rơi tự do hoặc ném vật trong không khí (khi không tính đến sức cản). Khi giải những bài tập này, chúng ta coi ‘g’ như là gia tốc ‘a’ trong các công thức chuyển động biến đổi đều quen thuộc. Nhờ có ‘g’, chúng ta có thể tính được sau bao lâu thì vật chạm đất, vận tốc của nó khi chạm đất là bao nhiêu, hoặc ném một vật lên cao thì nó đạt độ cao tối đa là bao nhiêu. Hiểu về gia tốc trọng trường giúp chúng ta giải mã được vô vàn hiện tượng xảy ra ngay xung quanh mình, từ quả táo rơi xuống đất đến quỹ đạo của một viên đạn bay đi.
Kết nối gia tốc, vận tốc, và quãng đường
À này, khi mà một vật không chạy đều đều nữa, mà tốc độ của nó cứ thay đổi ấy, thì chúng ta cần những công cụ "xịn sò" hơn để mô tả chuyển động của nó. Và đây chính là lúc gia tốc, vận tốc, và quãng đường bắt tay nhau trong những công thức cực kỳ hữu ích, đặc biệt là trong cái gọi là chuyển động biến đổi đều – tức là gia tốc không đổi theo thời gian.
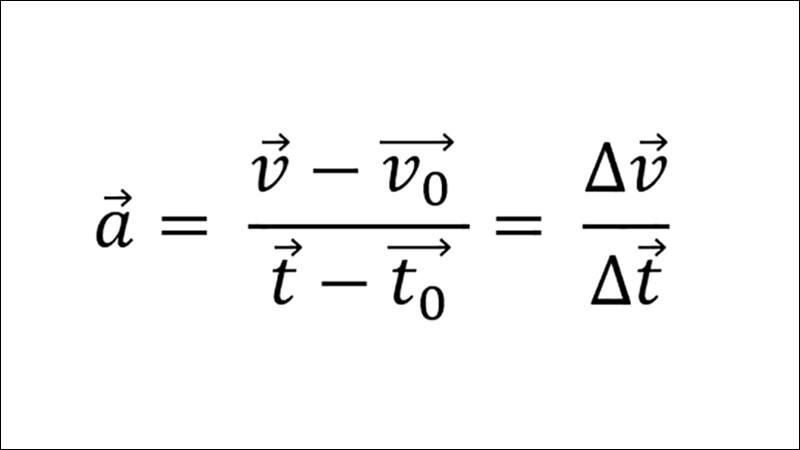
Tưởng tượng bạn đang lái xe và tăng tốc. Vận tốc của bạn đang thay đổi (có gia tốc). Bạn muốn biết sau bao lâu thì đạt được tốc độ mong muốn, hoặc đi được quãng đường bao xa trong lúc tăng tốc đó. Những công thức dưới đây chính là "kim chỉ nam" giúp bạn giải đáp những câu hỏi này.
Đầu tiên, mối liên hệ cơ bản nhất giữa sự thay đổi vận tốc và gia tốc theo thời gian:
v = v₀ + at
Công thức này nói rằng, vận tốc cuối (v) của bạn bằng vận tốc ban đầu (v₀) cộng thêm lượng vận tốc tăng thêm (hoặc giảm đi) do gia tốc (a) gây ra trong khoảng thời gian (t). Đơn giản mà hiệu quả, nó cho thấy gia tốc chính là "tốc độ" thay đổi của vận tốc.
Tiếp theo, nếu bạn quan tâm đến quãng đường đi được (s) trong quá trình vận tốc thay đổi, thì có công thức liên kết s với vận tốc ban đầu, gia tốc và thời gian:
s = v₀t + 1/2 at²
Công thức này hơi dài một chút nhưng nó cực kỳ mạnh mẽ. Nó cho biết tổng quãng đường đi được không chỉ phụ thuộc vào vận tốc ban đầu và thời gian, mà còn phụ thuộc vào gia tốc và thậm chí là bình phương của thời gian. Điều này giải thích tại sao khi tăng tốc, quãng đường bạn đi được trong giây tiếp theo lại lớn hơn giây trước đó.
Và đây là công thức "vàng" mà đề bài nhắc đến, nó liên kết vận tốc cuối, vận tốc đầu, gia tốc và quãng đường mà không cần biết thời gian:
v² - v₀² = 2as
Công thức này cực kỳ tiện lợi trong những bài toán mà thời gian không được cho hoặc không phải là thứ bạn cần tìm. Nó cho thấy bình phương vận tốc cuối trừ đi bình phương vận tốc đầu thì bằng hai lần gia tốc nhân với quãng đường đi được. Đây là một mối liên hệ trực tiếp và mạnh mẽ giữa tốc độ và khoảng cách trong chuyển động có gia tốc không đổi.
Những công thức này không chỉ là những dòng ký hiệu khô khan đâu nhé. Chúng là nền tảng để chúng ta phân tích và dự đoán chuyển động của mọi thứ xung quanh, từ viên bi lăn trên máng nghiêng, chiếc xe tăng tốc trên đường, cho đến những hành tinh quay quanh mặt trời (dù trường hợp này phức tạp hơn chút!). Nắm vững chúng chính là mở cánh cửa vào thế giới thú vị của cơ học cổ điển.
Gia tốc: Vận dụng ngay vào thực tế và bài tập
Học lý thuyết mãi cũng chán đúng không nào? Giờ thì xắn tay áo lên, mình cùng xem gia tốc "chạy" thế nào ngoài đời và làm sao để "bắt" nó vào bài tập nhé! Đây chính là lúc biến những công thức khô khan thành công cụ "xử đẹp" các bài toán vật lý và hiểu hơn về thế giới chuyển động quanh ta.

Bạn đã bao giờ ngồi trên ô tô, thấy bác tài đạp ga vọt lên chưa? Cái cảm giác "dính lưng" vào ghế ấy chính là gia tốc đang "làm việc" đấy. Hay khi bạn ném một quả bóng lên trời, nó bay chậm dần rồi rơi xuống nhanh dần, đó cũng là nhờ gia tốc trọng trường. Từ chiếc xe đạp đang tăng tốc trên dốc, viên bi lăn nhanh dần trên mặt phẳng nghiêng, cho đến tên lửa vụt bay vào không gian – tất cả đều là những ví dụ sống động về gia tốc. Hiểu gia tốc giúp chúng ta giải thích được tại sao mọi vật lại thay đổi vận tốc theo những cách thú vị như vậy.
Vật lý không chỉ mô tả bằng lời, mà còn dùng ngôn ngữ toán học để "đo đếm" chính xác sự thay đổi vận tốc này. Những công thức mà bạn vừa làm quen chính là "chìa khóa" để giải mã các tình huống chuyển động thực tế. Chẳng hạn, khi biết một vật bắt đầu chuyển động với vận tốc bao nhiêu, gia tốc của nó là bao nhiêu, bạn có thể dễ dàng tính được vận tốc của nó sau một khoảng thời gian nhất định hoặc quãng đường nó đi được. Ngược lại, nếu bạn đo được vận tốc ban đầu, vận tốc cuối và thời gian, bạn hoàn toàn có thể "truy ngược" ra gia tốc mà vật đó trải qua.
Khi gặp một bài toán về chuyển động có gia tốc, việc đầu tiên là "đọc vị" xem đề bài cho gì, hỏi gì. Vận tốc ban đầu bao nhiêu? Sau bao lâu thì vận tốc là bao nhiêu? Quãng đường đi được là bao nhiêu? Rồi mới chọn "vũ khí" phù hợp – tức là công thức liên hệ giữa các đại lượng đó. Đừng quên để ý đến chiều chuyển động và chiều của gia tốc nhé, vì dấu của chúng rất quan trọng đấy! Một gia tốc dương có thể làm vật chạy nhanh lên (nếu cùng chiều vận tốc) hoặc chậm lại (nếu ngược chiều vận tốc ban đầu âm), và ngược lại với gia tốc âm.
Giống như học bơi hay đi xe đạp, lý thuyết chỉ là khởi đầu. Bạn cần "nhảy xuống nước" và "đạp xe" thật nhiều. Bắt đầu với những bài tập đơn giản, quen thuộc, rồi tăng dần độ khó. Hãy thử sức với các bài toán về xe cộ tăng tốc/phanh gấp, vật rơi tự do, hay chuyển động trên mặt phẳng nghiêng. Mỗi lần áp dụng công thức, bạn sẽ thấy kiến thức dần "ngấm" vào mình. Đừng ngại sai, mỗi lần sai là một lần hiểu bài hơn và rút kinh nghiệm cho những lần sau.
Nắm vững cách vận dụng gia tốc không chỉ giúp bạn "xử đẹp" các bài kiểm tra mà còn giúp bạn hiểu hơn về thế giới chuyển động quanh mình. Từ việc tính toán thời gian một chiếc xe cần để đạt tốc độ mong muốn cho đến việc dự đoán quỹ đạo của một vật bị ném, gia tốc luôn đóng vai trò cốt lõi. Cứ luyện tập đều đặn, bạn sẽ thấy gia tốc không còn "khó nhằn" nữa đâu, mà trở thành một người bạn đồng hành thú vị trong hành trình khám phá vật lý.
