Bạn có bao giờ ngắm nhìn cánh bướm đang bay, bông tuyết sáu cánh hoàn hảo hay chỉ đơn giản là bóng mình soi dưới mặt nước phẳng lặng chưa? Tất cả những khoảnh khắc ấy đều gợi lên một cảm giác hài hòa, cân đối đến lạ kỳ – đó chính là đối xứng. Khái niệm này không chỉ xuất hiện trong những hình ảnh đẹp đẽ quanh ta mà còn ẩn chứa những ý nghĩa sâu sắc trong toán học, khoa học và nghệ thuật. Vậy, đối xứng thực sự là gì, và nó biểu hiện dưới những hình thức nào?
Đối xứng Vẻ Đẹp Cân Bằng Và Tính Bất Biến
Khi nói đến đối xứng, hình ảnh đầu tiên hiện lên trong đầu chúng ta thường là sự cân đối, hài hòa đến lạ lùng. Đó có thể là đôi cánh bướm rực rỡ, khuôn mặt người với hai bên gần như "ăn khớp" nhau, hay một tòa nhà cổ kính sừng sững với kiến trúc đăng đối. Trong ngôn ngữ đời thường, đối xứng gợi lên cảm giác dễ chịu, trật tự và vẻ đẹp thẩm mỹ. Nó là sự sắp xếp khéo léo, nơi các bộ phận dường như "nhìn nhau" qua một điểm hay một đường nào đó, tạo nên một tổng thể cân bằng, không lệch lạc. Cứ như thể có một "luật chơi" ngầm, đảm bảo mọi thứ được phân bổ thật hợp lý, tỷ lệ chuẩn chỉnh.

Nhưng dưới góc nhìn của toán học, khái niệm đối xứng không chỉ dừng lại ở cảm nhận thị giác hay sự hài hòa đơn thuần. Nó được định nghĩa một cách cực kỳ chính xác và chặt chẽ. Đối xứng trong toán học mô tả một tính chất đặc biệt của một đối tượng (có thể là hình, vật thể, phương trình, hay thậm chí là một tập hợp dữ liệu). Tính chất đó là sự bất biến – tức là không thay đổi – của đối tượng đó dưới một hoặc nhiều phép biến đổi nhất định.
Hãy hình dung thế này: bạn có một vật gì đó, rồi bạn thực hiện một "thao tác" lên nó, ví dụ như lật nó lại, xoay nó đi một góc nào đó. Nếu sau khi thực hiện thao tác ấy, vật đó vẫn trông y hệt như ban đầu, thì nó có tính đối xứng đối với thao tác đó. Khái niệm "phép biến đổi" ở đây không chỉ là di chuyển hay quay vật lý, mà là những quy tắc toán học làm thay đổi vị trí hoặc hướng của các điểm tạo nên đối tượng. Sự bất biến dưới các phép biến đổi này chính là cốt lõi làm nên định nghĩa toán học của đối xứng, một ý tưởng mạnh mẽ và sâu sắc hơn nhiều so với chỉ là "trông đẹp mắt" hay "cân bằng". Nó chính là nền tảng cho sự trật tự và quy luật trong thế giới hình học và hơn thế nữa.
Đối xứng trong hình học
Sau khi dạo quanh khái niệm đối xứng từ đời thường đến toán học, giờ là lúc chúng ta "phóng to" vào thế giới hình học đầy thú vị. Ở đây, đối xứng không chỉ là sự cân đối mắt thường nhìn thấy, mà còn là một tính chất đặc biệt liên quan đến các "phép biến hình" kỳ diệu. Tưởng tượng bạn lật một bức ảnh qua gương, hay xoay một vật thể quanh một điểm – nếu nó vẫn trông y hệt ban đầu, đó chính là lúc đối xứng hình học lên tiếng! Như Leonardo da Vinci đã tìm thấy sự đối xứng hoàn hảo trong cơ thể người, hình học cũng có những quy tắc riêng để tạo nên vẻ đẹp bất biến này. Vậy, những phép biến đổi nào giúp các hình giữ nguyên hình dáng và kích thước một cách thần kỳ như vậy? Chúng ta sẽ cùng khám phá ngay đây.
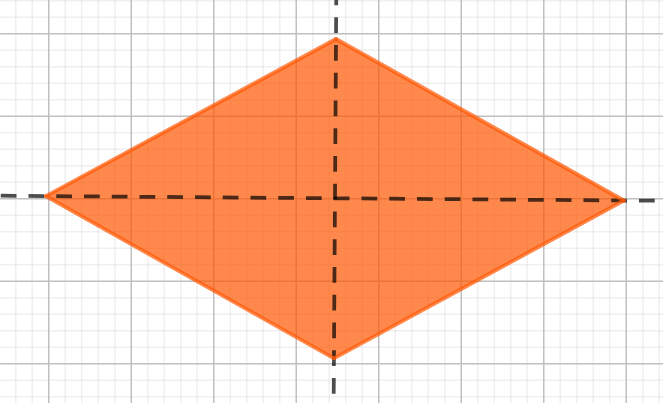
Khi hình ảnh soi gương
Tưởng tượng bạn đang đứng trước gương. Hình ảnh bạn thấy trong gương chính là "bản sao" của bạn, nhưng bị lật ngược lại. Đó là cách đơn giản nhất để hình dung về đối xứng trục trong hình học.
Bắt đầu với hai điểm nhé. Giả sử ta có điểm A và một đường thẳng ‘d’. Điểm A’ được gọi là đối xứng với điểm A qua đường thẳng ‘d’ nếu đường thẳng ‘d’ là trung trực của đoạn thẳng AA’. Nghe hơi "toán học" một chút, nhưng hiểu nôm na là: đoạn thẳng nối A và A’ phải vuông góc với đường thẳng ‘d’, và điểm cắt nhau ấy phải nằm chính giữa đoạn AA’. Giống như đường kẻ trên gương, nó nằm vuông góc với mặt đất và chia đôi khoảng cách từ bạn đến ảnh của bạn vậy.
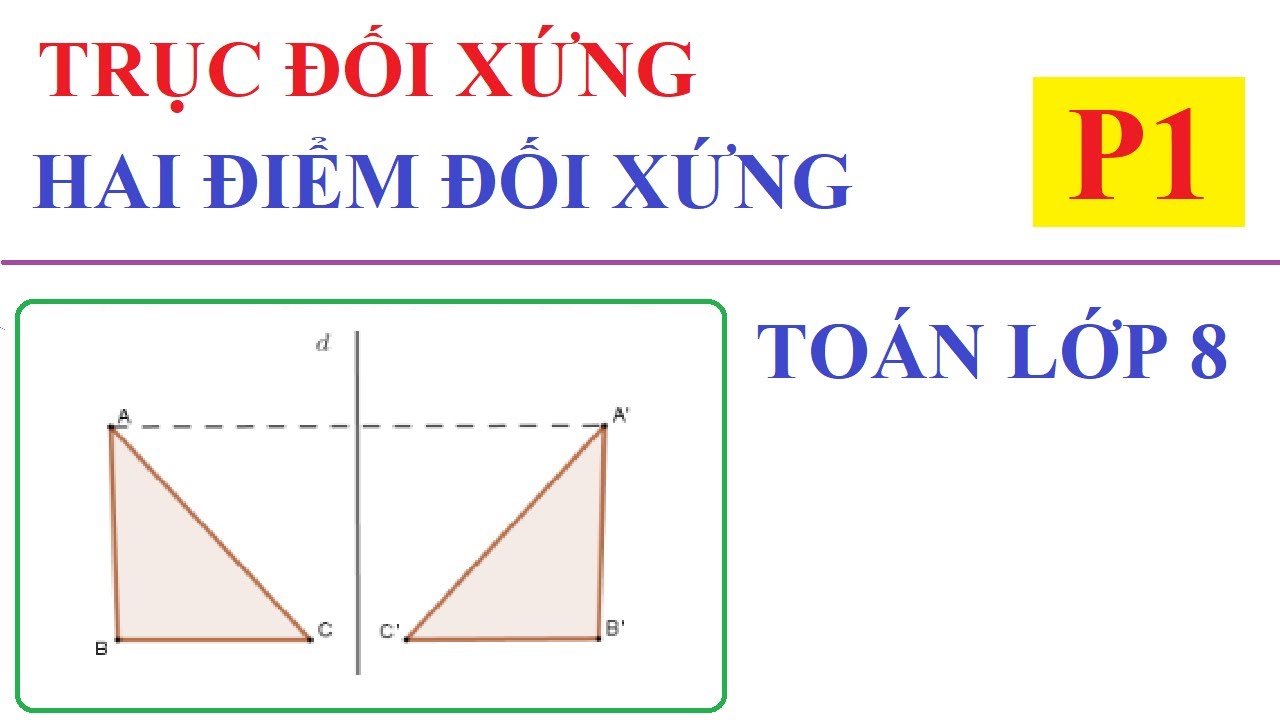
Vậy còn cả một hình thì sao? Khi ta nói hai hình H và H’ đối xứng với nhau qua đường thẳng ‘d’, điều đó có nghĩa là với mọi điểm M thuộc hình H, đều có một điểm M’ thuộc hình H’ sao cho M’ đối xứng với M qua đường thẳng ‘d’. Hình H’ chính là "ảnh" của hình H khi soi qua "gương" là đường thẳng ‘d’.
Nhưng có một trường hợp còn thú vị hơn: một hình có thể đối xứng với chính nó qua một đường thẳng nào đó. Đường thẳng đặc biệt này được gọi là trục đối xứng của hình. Nghĩa là, nếu bạn "gấp" hình đó lại theo đường thẳng này, hai nửa sẽ trùng khít lên nhau một cách hoàn hảo. Giống như đường gân chính giữa của một chiếc lá hay đường kẻ dọc trên khuôn mặt người vậy.
Điều kỳ diệu của phép đối xứng trục là nó bảo toàn hình dạng và kích thước. Hình ảnh trong gương của bạn vẫn là bạn, không cao hơn hay thấp đi, không béo hơn hay gầy đi. Tương tự, khi một hình được phản chiếu qua trục đối xứng, nó vẫn giữ nguyên mọi kích thước cạnh, góc, diện tích… Chỉ là nó bị lật lại thôi, tạo nên sự cân đối và hài hòa đáng kinh ngạc.
Đối xứng tâm: Quay quanh điểm giữa
Tưởng tượng nhé, bạn có một điểm O cố định. Bây giờ, lấy một điểm A bất kỳ. Nếu bạn vẽ một đường thẳng đi qua A và O, rồi kéo dài nó ra phía sau O một đoạn bằng đúng đoạn AO, bạn sẽ tìm được một điểm mới, gọi là A’. Điểm A’ này chính là điểm đối xứng với A qua điểm O. Đơn giản lắm, điểm O lúc này đóng vai trò là trung điểm của đoạn thẳng AA’. Nó nằm chính giữa, chia đôi đoạn thẳng ấy ra thành hai phần bằng nhau.
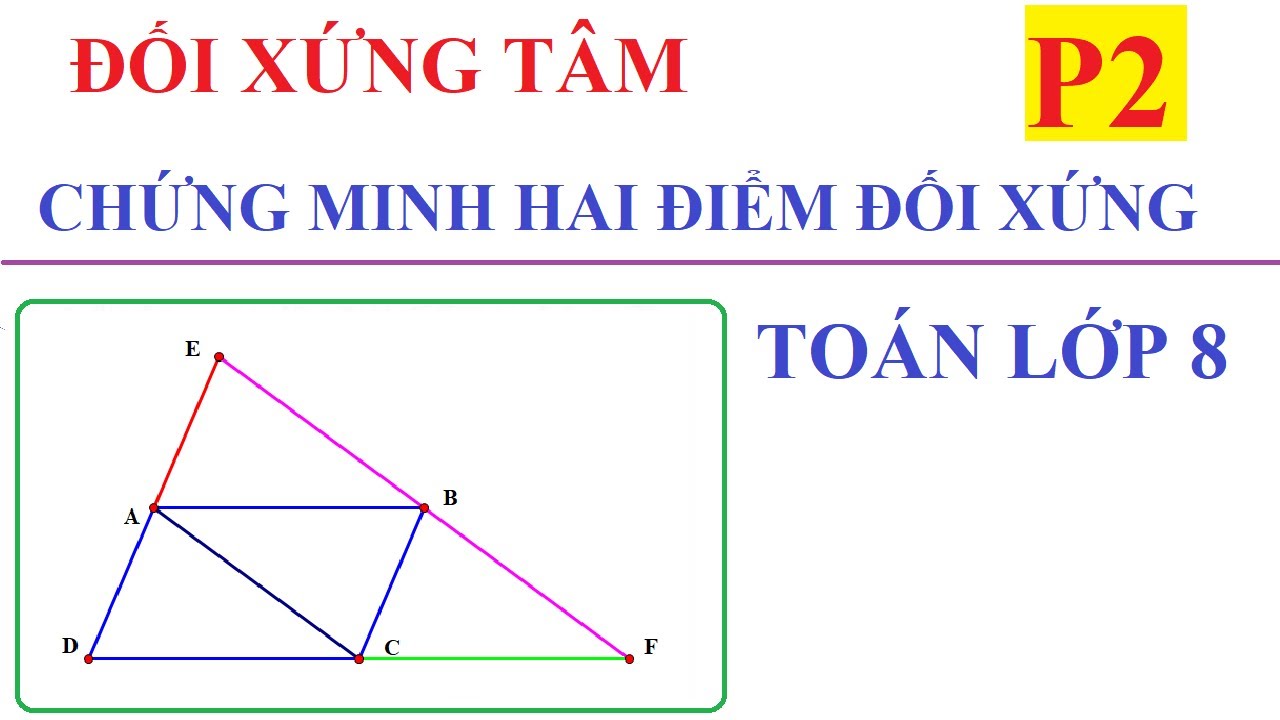
Vậy nếu không phải là một điểm mà là cả một hình? Chẳng hạn, bạn có một tam giác ABC. Áp dụng phép đối xứng qua điểm O cho từng đỉnh A, B, C, bạn sẽ nhận được ba điểm A’, B’, C’. Nối ba điểm này lại, bạn có tam giác A’B’C’. Tam giác A’B’C’ chính là hình đối xứng với tam giác ABC qua điểm O. Cứ mỗi điểm trên tam giác ABC đều có một "người anh em song sinh" đối xứng qua O nằm trên tam giác A’B’C’.
Điểm mấu chốt thú vị hơn là khi một hình lại đối xứng với chính nó qua một điểm nào đó. Lúc này, điểm đó được gọi là tâm đối xứng của hình. Nghĩa là, nếu bạn lấy bất kỳ điểm nào trên hình, tìm điểm đối xứng của nó qua tâm O, thì điểm đối xứng đó vẫn nằm gọn trong hình ban đầu. Cứ như thể bạn xoay hình đó một vòng 180 độ quanh điểm O, mà hình vẫn y nguyên, không suy suyển gì cả.
Phép đối xứng tâm này hay lắm ở chỗ nó giữ nguyên mọi thứ. Hình dạng không đổi, kích thước cũng không đổi. Một hình vuông đối xứng qua tâm vẫn là hình vuông kích thước cũ. Một đường tròn đối xứng qua tâm vẫn là đường tròn ấy. Đặc biệt, trong không gian hai chiều, đối xứng tâm còn bảo toàn cả định hướng. Khác với đối xứng trục là lật ngược như soi gương, đối xứng tâm giống như bạn quay hình đó đúng nửa vòng (180 độ) quanh tâm vậy. Mọi chi tiết vẫn giữ nguyên vị trí tương đối so với nhau, chỉ là cả hình bị "quay đầu" thôi.
Khám phá hình đối xứng
Đối xứng không chỉ là khái niệm khô khan trong sách vở đâu nhé. Nó hiện diện ngay trong những hình quen thuộc mà chúng ta gặp hàng ngày đấy. Cùng xem những "gương mặt" tiêu biểu nào sở hữu nét đẹp cân đối này nhé!
Bắt đầu với đối xứng trục nào. Nhắc đến đối xứng trục, hẳn bạn sẽ nghĩ ngay đến hình ảnh phản chiếu qua gương đúng không? Trong hình học, nhiều "ngôi sao" cũng có khả năng này.
Đơn giản nhất là tam giác cân. Em nó chỉ có một trục đối xứng duy nhất, chính là đường cao (hay trung tuyến, trung trực, phân giác) ứng với đỉnh đối diện cạnh đáy.
Hình thang cân cũng có một trục đối xứng, đi qua trung điểm hai đáy.
Hình thoi thì "giàu" hơn một chút, sở hữu tới hai trục đối xứng, chính là hai đường chéo của nó.
Hình chữ nhật cũng không kém cạnh với hai trục đối xứng, đi qua trung điểm của các cặp cạnh đối diện.
"Anh cả" hình vuông thì cực kỳ đối xứng, có tới bốn trục đối xứng lận: hai đường chéo và hai đường thẳng đi qua trung điểm các cặp cạnh đối diện.
Và "nữ hoàng" của sự đối xứng trục chính là đường tròn. Bạn biết không, đường tròn có vô số trục đối xứng! Bất kỳ đường kính nào đi qua tâm cũng đều là một trục đối xứng của nó. Thật kỳ diệu phải không?
Giờ chuyển sang đối xứng tâm nhé. Đối xứng tâm giống như quay 180 độ quanh một điểm vậy đó. Một số hình quen thuộc cũng có "điểm cân bằng" này.
Hình bình hành là một ví dụ điển hình, nó có một tâm đối xứng duy nhất, chính là giao điểm của hai đường chéo.
Các hình mà ta vừa nhắc đến ở phần đối xứng trục như hình chữ nhật, hình thoi, và hình vuông cũng đồng thời sở hữu một tâm đối xứng. Tâm này chính là giao điểm của hai đường chéo của chúng.
Và lại là đường tròn! Không chỉ có vô số trục đối xứng, đường tròn còn có một tâm đối xứng duy nhất, chính là tâm của nó.
Thấy chưa, thế giới hình học quanh ta thật phong phú và đầy những điều thú vị về sự cân đối, hài hòa!
Đối xứng Quanh Ta Khắp Chốn
Thoát khỏi những con số và hình vẽ khô khan, đối xứng hiện diện sống động ngay trong thế giới quanh ta, từ vẻ đẹp kỳ diệu của tự nhiên đến sự sáng tạo không ngừng nghỉ của con người trong nghệ thuật và những nguyên lý sâu xa của khoa học. Nó không chỉ mang lại cảm giác hài hòa, cân đối mà còn ẩn chứa những vai trò chức năng quan trọng.

Trong thế giới tự nhiên, đối xứng là một "ngôn ngữ" phổ biến. Hãy nhìn những cánh bướm sặc sỡ, cơ thể con người hay hầu hết các loài động vật khác – chúng ta đều thấy sự đối xứng hai bên rõ rệt. Kiểu đối xứng này giúp sinh vật di chuyển hiệu quả hơn, giữ thăng bằng tốt hơn và tương tác với môi trường một cách thuận lợi. Rồi những bông hoa xòe cánh, sao biển năm cánh hay những tinh thể lấp lánh lại thể hiện đối xứng tỏa tròn hay đối xứng hình học hoàn hảo, tạo nên vẻ đẹp khiến ta phải trầm trồ.
Bước vào thế giới nghệ thuật, đối xứng là một công cụ đắc lực để tạo nên sự cân bằng và ấn tượng thị giác. Từ kiến trúc cổ kính uy nghi như đền Taj Mahal với bố cục đối xứng tuyệt đối, mang lại cảm giác trang trọng, vĩnh cửu, đến những bức tranh, họa tiết trang trí sử dụng đối xứng để dẫn dắt ánh mắt người xem, tạo điểm nhấn và sự hài hòa tổng thể. Ngay cả trong âm nhạc, sự lặp lại có cấu trúc, các motif đối xứng cũng góp phần tạo nên sự mạch lạc, dễ nghe và đi sâu vào lòng người. Đối xứng mang lại cảm giác quen thuộc, dễ chịu, nhưng đôi khi, việc phá vỡ đối xứng một cách có chủ đích lại tạo nên sự độc đáo, kịch tính đầy thú vị.
Không chỉ dừng lại ở vẻ đẹp hình thức, đối xứng còn là nền tảng quan trọng trong khoa học. Trong vật lý, nhiều định luật cơ bản được xây dựng dựa trên các nguyên lý đối xứng, giúp các nhà khoa học hiểu sâu hơn về cách vũ trụ vận hành. Ví dụ, sự đối xứng của không gian và thời gian liên quan đến các định luật bảo toàn năng lượng và động lượng. Trong hóa học, hình dạng đối xứng của phân tử ảnh hưởng trực tiếp đến tính chất và cách chúng tương tác với nhau. Cấu trúc đối xứng của tinh thể quyết định độ bền, điểm nóng chảy và nhiều đặc tính vật lý khác của vật liệu.
Như vậy, đối xứng không chỉ là một khái niệm toán học trừu tượng. Nó là một phần không thể thiếu, định hình vẻ đẹp, chức năng và cấu trúc của thế giới xung quanh ta, từ những sinh vật nhỏ bé đến những công trình kiến trúc vĩ đại và cả những nguyên lý chi phối vũ trụ.

